数据结构和算法

算法引入

a + b + c = 1000 且 a^2 + b^2 = c^2，求出 a, b，c所有组合结果

思想：枚举法，列出所有可能结果

1
2
3
4
5
for a in range(1001):
	for b in range(1001):
		for c in range(1001):
			if a + b + c == 1000 and a**2 + b**2 == c**2:
				print(a, b, c)

优化

1
2
3
4
5
for a in range(1001):
	for b in range(1001):
		c = 1000 - a - b
		if a**2 + b**2 == c**2:
			print(a, b, c)

算法衡量

时间复杂度：程序的执行步骤

大O表示法：忽略常数项和次要项

最坏时间复杂度：程序最多执行多少个步骤

常见时间复杂度

img

注：img 为 img

顺序表

img

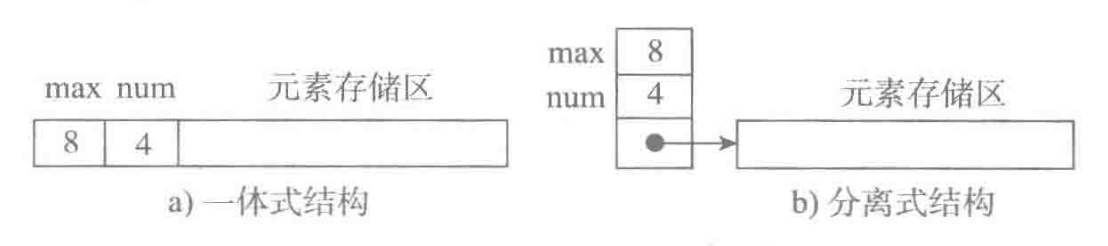
顺序表的两种基本实现方式

img

顺序表包含表头信息和元素存储区两部分

元素存储区扩充

两种扩充策略

每次扩充增加固定数目的存储位置，如每次扩充增加10个元素位置

每次扩充容量加倍，如每次扩充增加1倍存储空间

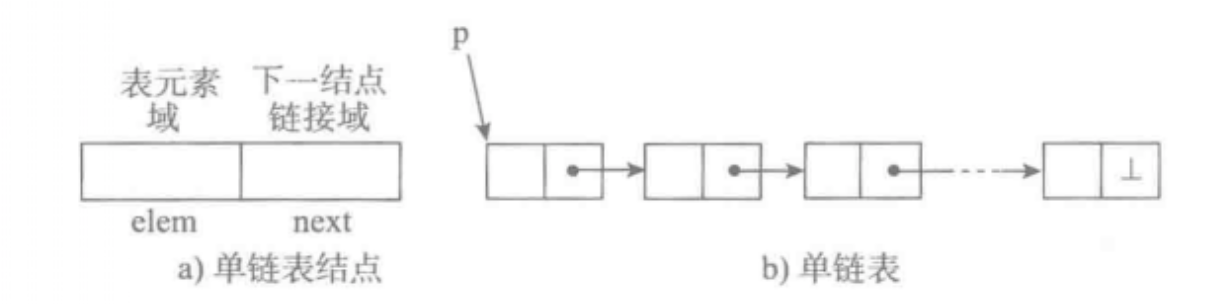
单链表

img

节点定义

1
2
3
4
class Node:
	def __init__(self, val):
		self.val = val
		self.next = None

单链表的定义

1
2
3
class SingleLinkList:
	def __init__(self, node=None):
		self.header = node

单链表操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
class Node:
	def __init__(self, val):
		self.val = val
		self.next = None

class SingleLinkList:
	
	def __init__(self, node=None):
		self.header = node

	def is_empty(self):
		return self.header == None

	def length(self):
		current = self.header
		count = 0
		while current != None:
			count += 1
			current = current.next

		return count

	def travel(self):
		current = self.header
		while current != None:
			print(current.val)
			current = current.next

	def append(self, val):

		current = self.header

		if current == None:
			self.header = Node(val)
		else:
			while current.next != None:
				current = current.next
			current.next = Node(val)

	def add(self, val):

		node = Node(val)

		if self.header == None:
			self.header = node
		else:
			node.next = self.header
			self.header = node


	def insert(self, pos, val):
		node = Node(val)
		current = self.header
		if pos == 0:
			node.next = current
			self.header = node
		elif pos >= self.length():
			self.append(val)
		else:
			current_pos = 0
			while current_pos != pos - 1:
				current_pos += 1
				current = current.next
			node.next = current.next
			current.next = node

	def remove(self, val):

		pre = None
		current = self.header
		while current.val != val:
			pre = current
			current = current.next
		if pre == None:
			self.header = current.next
		else:
			pre.next = current.next

	def search(self, val):

		current = self.header
		while current != None:
			if current.val == val:
				return True
			current = current.next
		return False

# 测试数据
s = SingleLinkList()
s.append(1)
s.append(2)
s.append(3)
s.add(5)
s.insert(1, 100)
s.remove(2)
print(s.travel())
print(s.search(5))

单向循环链表

双向链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
class Node:
	def __init__(self, val):
		self.val = val
		self.next = None
		self.prev = None

class DoubleLinkList:
	
	def __init__(self, node=None):
		self.header = node


	def travel(self):
		current = self.header
		while current != None:
			print(current.val)
			current = current.next

	def append(self, val):

		current = self.header
		node = Node(val)

		if current == None:
			self.header = node
		else:
			while current.next != None:
				current = current.next
			current.next = node
			node.prev = current

	def add(self, val):

		node = Node(val)

		if self.header == None:
			self.header = node
		else:
			node.next = self.header
			self.header = node
			node.next.prev = node


	def insert(self, pos, val):
		node = Node(val)
		current = self.header
		if pos == 0:
			node.next = current
			self.header = node
			node.next.prev = node
		elif pos >= self.length():
			self.append(val)
		else:
			current_pos = 0
			while current_pos != pos:
				current_pos += 1
				current = current.next

			node.next = current
			node.prev = current.prev
			current.prev = node
			current.prev.next = node


	def remove(self, val):

		current = self.header

		while current != None:
			if current.val == val:
				if current.prev is None:
					if current.next is not None:
						self.header = current.next
						current.next.prev = None
					else:
						self.header = None
				elif current.next is None:
					current.prev.next = None
				else:
					current.prev.next = current.next
					current.next.prev = current.prev
			current = current.next


d = DoubleLinkList()
d.append(1)
d.append(2)
d.append(3)
d.insert(0, 6)
d.remove(2)
d.travel()

栈

栈的数据结构实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Stack:
	def __init__(self):
		self.container = []

	def push(self, item):
		self.container.append(item)


	def pop(self):
		return self.container.pop()


	def peek(self):
		return self.container[-1]


	def size(self):
		return self.size()


	def is_empty(self):
		# if self.container == []:
		# 	return True
		# else:
		# 	return False

		return not self.container

s = Stack()
s.push(1)
s.push(2)
print(s.is_empty())

队列

java代码实现

python代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Queue:

	def __init__(self):
		self.container = []


	def enQueue(self, val):
		self.container.insert(0, val)


	def deQueue(self):
		return self.container.pop()



	def isEmpty(self):
		return not self.container


	def size(self):
		return len(self.container)



q = Queue()
q.enQueue(1)
print(q.deQueue())

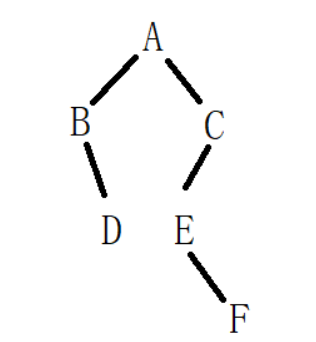
树

img

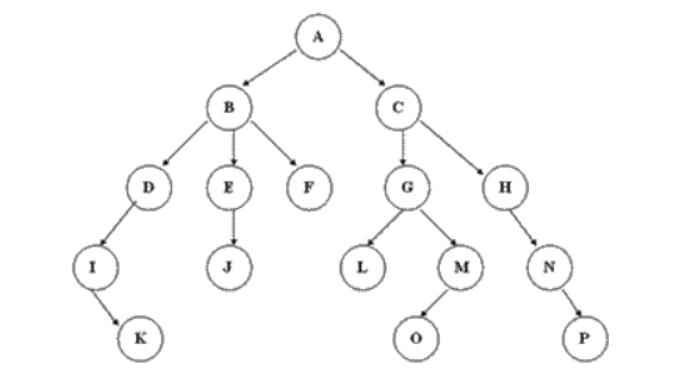
树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。每一个非空树都有且只有一个被称为根的结点

基本概念

（1）节点的度：一个节点含有的子树的个数称为该节点的度

如A节点的度为2、B节点的度为3

（2）树的度：一棵树中，最大的节点的度称为树的度

如上面这棵树的度为3

（3）叶子节点：度为0的节点

如K、F、O、P等都是叶子节点

（4）节点的层次：从根开始定义起，根为第1层，根的子节点为第2层

上面这颗树一共有5层

（5）树的高度或深度：树中节点的最大层次

上面这颗树的高度或深度为5

（6）森林：由m（m>=0）棵互不相交的树的集合称为森林

二叉树

二叉树：每个节点最多含有两个子树的树称为二叉树

几个性质

（1）在二叉树的第img层上至多有个img结点（i>0）

（2）深度为img的二叉树至多有个img结点

（3）对于任意一棵二叉树，如果其叶结点数为img，而度数为2的结点总数为img，则img

（4）具有img个结点的满二叉树的深度为img

（5）对完全二叉树，若从上至下、从左至右编号，则编号为i的结点，其左孩子编号必为img，其右孩子编号必为img

完全二叉树

设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树

img

满二叉树

img

平衡二叉树

当且仅当任何节点的两棵子树的高度差不大于1的二叉树

排序二叉树

从根节点按照编号，从左到右进行编号

2-3-4树

红黑树

B树

霍夫曼树

遍历

前序、中序、后序

img

依据前序和中序或者前序和后序可以完整的构建出一颗二叉树

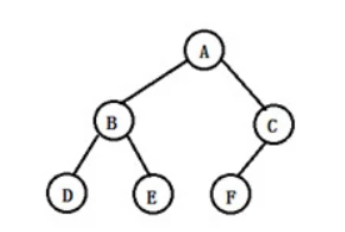
前序：A B D C E F

中序：B D A E F C

（1）确定根A

（2）依据中序A所在位置划分左右两颗子树

img

后序：D B F E C A

中序：B D A E F C

（1）确定根的位置A

（2）依据中序划分左右两颗子树

冒泡

思路分析

比较前后两个数, 如果前面一个数比后面一个数大, 则交换位置。

python示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
arr = [1, 100, 35, 56, 72, 5, 3, 2]


def bubble_sort(arr):
	"""冒泡排序"""
	pythonj = (len(arr) - 2)

	while j != 0:
		flag = 0
		i = 0
		while i != j:
			if arr[i] > arr[i+1]:
				arr[i], arr[i+1] = arr[i+1], arr[i]
				flag += 1
			i += 1
		if arr[i] > arr[i+1]:
				arr[i], arr[i+1] = arr[i+1], arr[i]
				flag += 1
		if flag == 0:
			return
		j -= 1
		
bubble_sort(arr)
print(arr)

java版本示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class HelloWorld{
    public static void main(String[] args){

        // 给定一个数组
        int[] arr = {1, 5, 2, 7, 9};

        // 冒泡排序
        // 数组长度
        int len = arr.length;

        // 产生一个序列, 4 3 2
        for(int j=len-1; j>=2; j--){
            // 比较前后两个数, 如果前面一个数比后面一个数大, 则交换位置。
            for(int i=0; i<j; i++){
                if(arr[i] > arr[i+1]){
                    // 交换位置
                    int temp = arr[i + 1];
                    arr[i+1] = arr[i];
                    arr[i] = temp;
                }
            }
        }

        // 遍历数组, 测试结果是否正确
        for(int i=0; i<len; i++){
            System.out.println(arr[i]);
        }
    }    
}

选择

思路分析

打擂台算法，每次都找到最大值或最小值, 与数组最后一个元素交换位置。

python示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
arr = [4, 100, 35, 56, 72, 5, 3, 1]


def select(arr):
	"""选择排序"""

	j = 0

	while j != (len(arr) - 1):
		min_index = j
		start = j
		index = j + 1
		while index != (len(arr) - 1):
			if arr[min_index] > arr[index]:
				min_index = index
			index += 1
		# 比较数组中最后一个值
		if arr[min_index] > arr[index]:
				min_index = index

		arr[start], arr[min_index] = arr[min_index], arr[start]
		j += 1


select(arr)
print(arr)

java代码示例如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class HelloWorld{
    public static void main(String[] args){

        // 给定一个数组
        int[] arr = {1, 100, 2, 7, 9};

        // 选择排序
        // 数组长度
        int len = arr.length;

        // 产生一个序列, 5 4 3 2, 控制循环
        for(int j=len; j>=2; j--){

            // 打擂台算法, 找到最大值, 与数组最后一个值交换。
            int maxIndex = 0;
            for(int i=1; i<j; i++){
                if(arr[i] > arr[maxIndex]){
                    maxIndex = i;
                }
            }

            // 如果数组最后一个数恰好是最大值, 否则不用交换。
            if(maxIndex != j-1){
                // 交换位置
                int temp = arr[j - 1];
                arr[j - 1] = arr[maxIndex];
                arr[maxIndex] = temp;
            }
        }

        // 遍历数组, 测试结果是否正确
        for(int i=0; i<len; i++){
            System.out.println(arr[i]);
        }
    }    
}

插入

示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
arr = [100, 4, 35, 23, 72, 5, 3, 1]


def insert_sort(arr):
	"""插入排序"""

	index = 1
	while index != len(arr):
		start = index
		while start != 0:
			if arr[start] < arr[start - 1]:
				arr[start], arr[start - 1] = arr[start - 1], arr[start]
			start -= 1
		index += 1

insert_sort(arr)
print(arr)

二分

java示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
package com.cskaoyan;

import java.util.Scanner;

public class Demo {

    public static void main(String[] args){

        // 给定一个有序的数组
        int[] arr = {1, 4, 11, 18, 19};
        
        int index = binarySearch(arr, 17);

        System.out.println(index);

    }

    // 二分查找算法
    public static int binarySearch(int[] arr, int num){

        int left = 0;
        int right = arr.length - 1;
        int mid = (left + right) / 2;

        while(true){
            if(arr[mid] == num){
                return mid;
            }
            if(arr[mid] > num){

                // 更新表达式
                right = mid - 1;

            }else{
                // 更新表达式
                left = mid + 1;
            }

            mid = (left + right) / 2;

            if(left > right){
                // 找不到想要的元素
                return -1;
            }
        }
    }

}

数字累加

计算1到100之和

循环

1
2
3
4
5
6
7
public static int sum(int n) {
    int sum = 0;
    for(int i=1; i<=n; i++){
        sum+=i;
    }
    return sum;
}

其他解法

1
2
3
public static int sum(int n) {
    return (1 + n) * n / 2;
}

斐波那契

0 1 1 2 3 5 8 13

求第n个斐波那契数列的值

递归

1
2
3
4
5
6
public static int fio(int n) {
    if(n <= 2){
        return n - 1;
    }
    return fio(n-1) + fio(n-2);
}

循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int fio(int n) {
    if(n <= 2){
        return n - 1;
    }
    int first = 0;
    int second = 1;

    for(int i=0; i<n-2; i++){

        int sum = first + second;

        // 更新表达式
        first = second;
        second = sum;
    }
    return second;
}

从上到下打印二叉树

示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {

        if(root == null) return new ArrayList();

        // 创建一个二维数组
        List<List<Integer>> arrayList = new ArrayList();
        // 创建一个队列
        Queue<TreeNode> queue = new LinkedList();

        queue.add(root);

        // 当前层数是否为奇数
        boolean isOdd = false;

        // 队列不为空
        while(!queue.isEmpty()){
            // 当前层数节点数
            int size = queue.size();
            // 创建一个临时的一维数组
            LinkedList<Integer> temp = new LinkedList();
            for(int i=0; i<size; i++){

                TreeNode node = queue.poll();

                if(isOdd){
                    temp.addFirst(node.val);
                }else{
                    temp.addLast(node.val);
                }
                
                // 判断左右节点
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
                
            }
            arrayList.add(temp);
            isOdd = !isOdd;
        }
        return arrayList;
    }
}

从上到下打印二叉树

示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {

        if(root == null) return new ArrayList();

        // 创建一个二维数组, 里面是一个一维数组
        List<List<Integer>> listArray = new ArrayList();
        // 创建一个队列
        Queue<TreeNode> queue = new LinkedList();
        // 添加根节点
        queue.add(root);
        // 队列不为空
        while(!queue.isEmpty()){

            // 当前队列中的节点数
            int size = queue.size();

            // 临时数组
            ArrayList<Integer> temp = new ArrayList();

            for(int i=0; i<size; i++){
                TreeNode node = queue.poll();
                temp.add(node.val);
                // 判断左右节点
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            listArray.add(temp);
        }
        return listArray;
    }
}

示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] levelOrder(TreeNode root) {

        if(root == null) return new int[0];

        // 动态数组
        ArrayList<Integer> arrayList = new ArrayList();
        // 创建一个队列
        Queue<TreeNode> queue = new LinkedList();
        // 入队
        queue.add(root);
        while(!queue.isEmpty()){
            TreeNode node =  queue.poll();
            arrayList.add(node.val);
            // 判断是否有左右节点
            if(node.left != null){
                queue.add(node.left);
            }
            if(node.right != null){
                queue.add(node.right);
            }
        }
        // 遍历arrayList
        int[] res = new int[arrayList.size()];
        int index = 0;
        for(Integer i : arrayList){
            res[index++] = i;
        }
        return res;
    }
}

只出现一次字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public char firstUniqChar(String s) {

        // 利用HashMap解题
        HashMap<Character, Integer> hashMap = new HashMap();
        // 遍历字符串
        for(int i=0; i<s.length(); i++){
            char c = s.charAt(i);
            if(!hashMap.containsKey(c)){
                hashMap.put(c, 1);
            }else{
                int val = hashMap.get(c);
                hashMap.put(c, val+1);
            }
        }
        // 再次遍历字符串
        for(int i=0; i<s.length(); i++){
            char c = s.charAt(i);
            if(hashMap.get(c) == 1){
                return c;
            }
        }
        return ' ';
    }
}

二维数组

示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {

        // 从左下角开始扫描
        int row = matrix.length - 1;
        int column = 0;
        while(row >= 0 && column < matrix[0].length){
            if(matrix[row][column] == target){
                return true;
            }
            if(matrix[row][column] > target){
                row--;
            }else{
                column++;
            }
        }
        return false;
    }
}
数据结构和算法
http://cxycsx.vip/2023/08/31/其他/数据结构和算法/
作者
程序员陈师兄
发布于
2023年8月31日
许可协议